Elastinen lineaarinen regressio käyttää sekä lasso- että harjanteen tekniikoiden seuraamuksia regressiomallien laillistamiseen. Tekniikka yhdistää sekä lassoa että LASSO LASSO, lyhenne sanoista Least Absolute Shrinkage and Selection Operator, on tilastollinen kaava, jonka päätarkoitus on ominaisuuksien valinta ja säännöllisyys sekä harjanteen regressiomenetelmät oppimalla niiden puutteista tilastomallien säännöllisyyden parantamiseksi.
Joustavan verkon menetelmä parantaa lason rajoituksia, toisin sanoen, kun lasso ottaa muutaman näytteen korkean ulottuvuuden dataa varten, joustavan verkon menettely tarjoaa "n" muuttujien lukumäärän kyllästykseen asti. Siinä tapauksessa, että muuttujat ovat voimakkaasti korreloivia ryhmiä, lasso pyrkii valitsemaan yhden muuttujan tällaisista ryhmistä ja sivuuttamaan loput kokonaan.
Lassoissa havaittujen rajoitusten poistamiseksi joustava verkko sisältää rangaistuksessa toisen asteen lausekkeen (|| β || 2), josta erillisenä käytettynä tulee harjanteen regressio. Rangaistuksen neliöllinen ilmaisu nostaa menetystoimintoa kohti kuperaa. Joustava verkko perustuu molempien maailmojen parhaisiin osiin - ts. Lason ja harjanteen regressioon.
Elastisen verkkomenetelmän estimaattorin löytämisessä on kaksi vaihetta, jotka sisältävät sekä lasso- että regressiotekniikkaa. Se löytää ensin harjanteen regressiokertoimet ja suorittaa sitten toisen vaiheen käyttämällä lasojen eräänlaista kutistumista.
Siksi tämä menetelmä kertoo kertoimet kahdessa kutistumistyypissä. Kaksoiskutistuminen joustavan verkon naiivista versiosta aiheuttaa heikkoa ennustettavuutta ja suurta puolueellisuutta. Tällaisten vaikutusten korjaamiseksi kertoimet skaalataan uudelleen kertomalla ne (1 + λ2).
Nopea yhteenveto
- Joustavan verkon menetelmä suorittaa muuttuvan valinnan ja säätämisen samanaikaisesti.
- Joustavan verkon tekniikka on sopivin, kun mittatiedot ovat suurempia kuin käytettyjen näytteiden lukumäärä.
- Ryhmittely ja muuttujien valinta ovat joustavan verkon tekniikan keskeisiä rooleja.
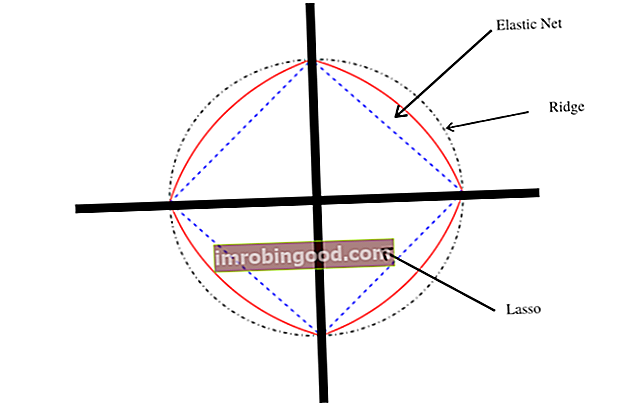
Elastinen verkkogeometria
Kartesiaaniselle tasolle piirrettynä joustava verkko putoaa harjanteen ja lason regressiokaavioiden väliin, koska se on näiden kahden regressiomenetelmän yhdistelmä. Joustavan verkon juoni osoittaa myös huippupisteissä singulariteettia, mikä on tärkeää harvinaisuuden kannalta. Sillä on myös tiukat kuperat reunat, joissa kuperuus riippuu a: n arvosta.
Koveruus riippuu myös korrelaatiosta riippuvasta ryhmittelyvaikutuksesta Korrelaatio Korrelaatio on tilastollinen mitta kahden muuttujan välisestä suhteesta. Mittaria käytetään parhaiten muuttujissa, jotka osoittavat lineaarisen suhteen toistensa välillä. Datan sopivuus voidaan visuaalisesti edustaa hajontakaaviona. valituista muuttujista. Mitä korkeampi muuttujien korrelaatio, sitä suurempi ryhmittelyvaikutus on, ja sitä suurempi on otokseen sisältyvien muuttujien lukumäärä.
Muuttujien valinta
Mallin rakentaminen edellyttää muuttujien valintaa ennustajien osajoukon muodostamiseksi. Elastinen verkko käyttää p >> n-ongelman lähestymistapaa, mikä tarkoittaa, että ennustajien lukumäärä on suurempi kuin mallissa käytettyjen näytteiden määrä. Joustava netto on tarkoituksenmukainen, kun muuttujat muodostavat ryhmiä, jotka sisältävät erittäin korreloivia riippumattomia muuttujia Itsenäinen muuttuja Riippumaton muuttuja on syöte, oletus tai ohjain, jota muutetaan sen vaikutuksen arvioimiseksi riippuvaan muuttujaan (lopputulokseen). .
Muuttujavalinta on sisällytetty mallinrakennusprosessiin tarkkuuden lisäämiseksi. Siinä tapauksessa, että muuttujaryhmä korreloi voimakkaasti ja yksi muuttujista valitaan otokseen, koko ryhmä sisällytetään automaattisesti otokseen.
CATREG-yhtiö
CATREG on algoritmi, joka helpottaa muuttujien, sekä lineaaristen että epälineaaristen, muunnosta. Algoritmi hyödyntää vaihe- ja spline-funktioita muuttujien muuttamisessa joko ei-monotonisesti tai monotonisesti epälineaarisissa muunnoksissa. CATREG voi samanaikaisesti muuntaa ja laillistaa muuttujia ei-monotonisesti tarvitsematta välttämättä ensin laajentaa muuttujia perustoimintoiksi tai nukkeiksi.
Elastisia nettohäviöfunktioita voidaan kutsua myös tavallisen pienimmän neliösumman regressiohäviöfunktion rajoitetuksi tyypiksi. CATREG-algoritmi on sisällytetty joustavaan verkkoon, mikä parantaa tuloksena olevan algoritmin tehokkuutta ja yksinkertaisuutta. Vertailun vuoksi elastinen verkko ylittää lason, joka itse ylittää harjanteen regressio tehokkuuden ja yksinkertaisuuden suhteen.
Elastinen nettoregulaatio
Laillistamismenettelyn aikana l1 rangaistuksen osa muodostaa harvan mallin. Toisaalta rangaistuksen neliöllinen osa tekee l1 osa vakaampi säännöllisyyden polulla, eliminoi valittavien muuttujien määrällisen rajoituksen ja edistää ryhmittelyvaikutusta.
Ryhmävaikutus auttaa muuttujia tunnistamaan helposti korrelaation avulla. Se parantaa näytteenottomenettelyä. Se lisää myös valittujen muuttujien lukumäärää, koska kun yhdestä muuttujasta otetaan näyte erittäin korreloivassa ryhmässä, kaikki muut ryhmän muuttujat lisätään automaattisesti otokseen.
Tehokkaat vapausasteet
Tehokkaat vapausasteet mittaavat mallin monimutkaisuutta. Vapausasteet ovat tärkeitä mallin sovituksen arvioinnin tai tarkan ennustamisen aikana. Vapauden asteet sisällytetään myös lineaaristen tasoittajien oppimiseen. Missä tahansa menetelmään, joka liittyy l1 rangaistus, mallien epälineaarisuus aiheuttaa haasteen analyysissä.
Elastista verkkoa voidaan käyttää myös muissa sovelluksissa, kuten harvassa PCA: ssa, jossa se saa pääkomponentit, joita muokkaavat harvat kuormitukset. Toinen sovellus on ytimen joustavassa verkossa, jossa luokan ydinkoneiden sukupolvi tapahtuu tukivektoreilla.
Lisäresurssit
Rahoitus tarjoaa Certified Banking & Credit Analyst (CBCA) ™ CBCA ™ -sertifikaatin Certified Banking & Credit Analyst (CBCA) ™ -sertifikaatti on maailmanlaajuinen luottotietojen analyytikoiden standardi, joka kattaa rahoituksen, kirjanpidon, luottotutkimukset, kassavirta-analyysit, kovenanttimallinnukset, lainat takaisinmaksut ja paljon muuta. sertifiointiohjelma niille, jotka haluavat viedä uransa seuraavalle tasolle. Tutki alla olevia asiaankuuluvia muita rahoitusresursseja jatkaaksesi oppimista ja tietopohjan kehittämistä:
- Päätöspuu Päätöspuu Päätöspuu on puumaisen rakenteen omaava tukityökalu, joka mallinnaa todennäköiset tulokset, resurssikustannukset, apuohjelmat ja mahdolliset seuraukset.
- Riippuva muuttuja Riippuva muuttuja Riippuva muuttuja on muuttuja, joka muuttuu toisen muuttujan, riippumattoman muuttujan, arvosta riippuen.
- Moninkertainen lineaarinen regressio Moninkertainen lineaarinen regressio Moninkertainen lineaarinen regressio viittaa tilastolliseen tekniikkaan, jota käytetään riippuvan muuttujan tuloksen ennustamiseen riippumattomien muuttujien arvon perusteella
- Overfitting Overfitting Overfitting on tilastoissa käytetty termi, joka viittaa mallinnusvirheeseen, joka tapahtuu, kun toiminto vastaa liian tarkasti tiettyä tietojoukkoa

