Kovarianssi - määritelmä, kaava ja käytännön esimerkki

Matematiikassa ja tilastoissa Rahoituksen perustilastokäsitteet Tilastojen vahva ymmärtäminen on ratkaisevan tärkeää, jotta voimme paremmin ymmärtää taloutta. Lisäksi tilastokäsitteet voivat auttaa sijoittajia seuraamaan, kovarianssi on mittari kahden satunnaismuuttujan välisestä suhteesta. Mittari arvioi, kuinka paljon - missä määrin - muuttujat muuttuvat yhdessä. Toisin sanoen, se on olennaisesti kahden muuttujan välisen varianssin mitta. Mittari ei kuitenkaan arvioi muuttujien välistä riippuvuutta.

Kovarianssia mitataan yksiköinä, toisin kuin korrelaatiokerroin. Yksiköt lasketaan kertomalla kahden muuttujan yksiköt. Varianssi voi olla mikä tahansa positiivinen tai negatiivinen arvo. Arvot tulkitaan seuraavasti:

• Positiivinen kovarianssi: Ilmaisee, että kahdella muuttujalla on taipumus liikkua samaan suuntaan.
• Negatiivinen kovarianssi: Paljastaa, että kahdella muuttujalla on taipumus liikkua käänteissuuntaan.

Rahoituksessa Finance Finance -yhtiön Finance-artikkelit on suunniteltu itsenäisiksi opiskeluoppaiksi tärkeiden rahoituskäsitteiden oppimiseksi verkossa omaan tahtiisi. Selaa satoja artikkeleita! , käsitettä käytetään ensisijaisesti salkuteoriassa. Yksi sen yleisimmistä sovelluksista salkuteoriassa on hajauttaminen Hajauttaminen Hajauttaminen on tekniikka, jolla kohdennetaan salkun resursseja tai pääomaa erilaisiin sijoituksiin. Hajauttamisen tavoitteena on vähentää tappioita -menetelmää käyttämällä salkun omaisuuden kovarianssia. Valitsemalla omaisuuserät, joilla ei ole kovaa positiivista kovarianssia toistensa kanssa, systemaattinen riski voidaan osittain eliminoida.

Rahoitus Matematiikka yritysrahoituskurssille tutkii taloudellisen mallinnuksen edellyttämiä finanssimatematiikan käsitteitä. Mikä on taloudellinen mallinnus Taloudellinen mallinnus suoritetaan Excelissä yrityksen taloudellisen suorituskyvyn ennustamiseksi. Katsaus taloudelliseen mallintamiseen, miten ja miksi malli rakennetaan.

Kovarianssin kaava

Kovarianssikaava on samanlainen kuin korrelaatiokaava ja käsittelee datapisteiden laskemista tietojoukon keskiarvosta. Esimerkiksi kahden satunnaismuuttujan X ja Y välinen kovarianssi voidaan laskea käyttämällä seuraavaa kaavaa (populaatiolle):

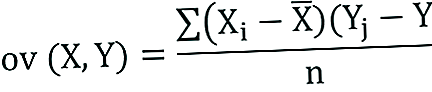
Kovarianssinäytettä varten kaavaa mukautetaan hieman:

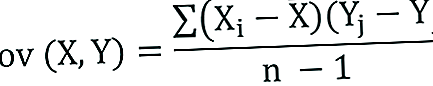
Missä:

• X_i - X-muuttujan arvot
• Y_j- Y-muuttujan arvot
• X̄ - X-muuttujan keskiarvo (keskiarvo)
• Ȳ - Y-muuttujan keskiarvo (keskiarvo)
• n - datapisteiden lukumäärä

Kovarianssi vs. korrelaatio

Kovarianssi ja korrelaatio arvioivat molemmat ensisijaisesti muuttujien välistä suhdetta. Lähin analogia niiden väliseen suhteeseen on varianssin ja keskihajonnan välinen suhde. Keskihajonta Tilastollisesta näkökulmasta tietojoukon keskihajonta mittaa sisältämien havaintojen arvojen välisten poikkeamien suuruutta.

Kovarianssi mittaa kahden satunnaismuuttujan kokonaisvaihtelun odotetuista arvoista. Kovarianssia käyttämällä voimme vain mitata suhteen suuntaa (onko muuttujilla taipumus liikkua tandemina vai käänteisen suhteen). Se ei kuitenkaan osoita suhteen suhdetta eikä muuttujien välistä riippuvuutta.

Toisaalta, korrelaatio mittaa muuttujien välisen suhteen voimakkuutta. Korrelaatio on kovarianssin mittakaava. Se on ulottumaton. Toisin sanoen korrelaatiokerroin on aina puhdas arvo eikä sitä mitata missään yksikössä.

Kahden käsitteen suhde voidaan ilmaista seuraavalla kaavalla:

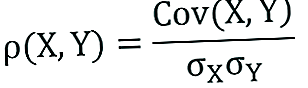
Missä:

• ρ (X, Y) - muuttujien X ja Y välinen korrelaatio
• Cov (X, Y) - kovarianssi muuttujien X ja Y välillä
• σ_X - X-muuttujan keskihajonta
• σ_Y- Y-muuttujan keskihajonta

Esimerkki kovarianssista

John on sijoittaja. Hänen salkunsa seuraa ensisijaisesti S&P 500: n kehitystä ja John haluaa lisätä ABC Corp: n osakekannan. Ennen kuin lisäät osakkeen salkkuunsa, hän haluaa arvioida osakekannan ja S&P 500: n suunnan suhteen.

John ei halua lisätä salkunsa systemaattista riskiä. Siksi hän ei ole kiinnostunut omistamaan salkkuun arvopapereita, joilla on taipumus liikkua samaan suuntaan.

John voi laskea kovarianssin ABC Corp.: n ja S&P 500: n osakkeiden välillä seuraamalla seuraavia vaiheita:

1. Hanki tiedot.

Ensinnäkin John hankkii sekä ABC Corp. -osakkeen että S&P 500: n luvut. Saadut hinnat on esitetty yhteenvetona alla olevassa taulukossa:

2. Laske kunkin omaisuuden keskimääräiset (keskimääräiset) hinnat.

3. Etsi kunkin arvopaperin arvo kunkin keskiarvon ja keskihinnan välillä.

4. Kerro edellisessä vaiheessa saadut tulokset.

5. Etsi kovarianssi käyttämällä vaiheessa 4 laskettua lukua.

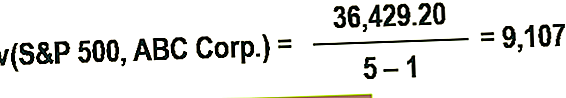
Tällöin positiivinen kovarianssi osoittaa, että osakkeen hinta ja S&P 500 liikkuvat yleensä samaan suuntaan.

Lisäresurssit

Finance tarjoaa Financial Modeling & Valuation Analyst (FMVA) ™ FMVA® -sertifikaatin. Liity 350 600+ opiskelijaan, jotka työskentelevät yrityksissä, kuten Amazon, J.P.Morgan ja Ferrari -sertifikaattiohjelmassa, niille, jotka haluavat viedä uransa seuraavalle tasolle. Seuraavat rahoitusresurssit ovat hyödyllisiä oppimisen jatkamiseksi ja urasi edistämiseksi:

• Sijoittaminen: Aloittelijan opas Sijoittaminen: Aloittelijan opas Talouden sijoittaminen aloittelijoille -opas opettaa sinulle sijoittamisen perusteet ja miten pääset alkuun. Tutustu erilaisiin kaupankäynnin strategioihin ja tekniikoihin sekä eri rahoitusmarkkinoihin, joihin voit sijoittaa.
• Negatiivinen korrelaatio Negatiivinen korrelaatio Negatiivinen korrelaatio on suhde kahden vastakkaiseen suuntaan liikkuvan muuttujan välillä. Toisin sanoen, kun muuttuja A kasvaa, muuttuja B pienenee. Negatiivinen korrelaatio tunnetaan myös käänteisenä korrelaationa. Katso esimerkkejä, kaavioita ja
• Riski ja tuotto Riski ja tuotto Sijoituksessa riski ja tuotto korreloivat voimakkaasti. Potentiaalisen sijoitetun pääoman tuoton nousu liittyy yleensä lisääntyneeseen riskiin. Erilaisia ​​riskejä ovat projektikohtainen riski, toimialakohtainen riski, kilpailuriski, kansainvälinen riski ja markkinariski.
• Riskienhallinta Riskienhallinta Riskienhallinta sisältää tunnistamisen, analysoinnin ja vastaamisen riskitekijöihin, jotka ovat osa yrityksen elämää. Se tehdään yleensä