Säädetty R-neliö on muokattu versio R-neliöstä, joka ottaa huomioon ennustimet, joilla ei ole merkitystä regressiomallissa. Toisin sanoen, oikaistu R-neliö osoittaa, parantaako lisäennusteita lisäämällä regressiomallia vai ei. Mukautetun R-neliön ymmärtäminen edellyttää R-neliön ymmärtämistä.
Yhteenveto:
- Säädetty R-neliö on R-neliön muunnettu versio, joka säätyy ennustajille, joilla ei ole merkitystä regressiomallissa.
- Verrattuna malliin, jossa on muita syöttömuuttujia, pienempi säädetty R-neliö osoittaa, että lisäpanosmuuttujat eivät tuota arvoa mallille.
- Verrattuna malliin, jossa on muita syöttömuuttujia, korkeampi säädetty R-neliö osoittaa, että lisäpanosmuuttujat lisäävät arvoa malliin.
Mikä on R-neliö?
R-neliötä, jota kutsutaan myös määrityskertoimeksi Määrityskerroin Määrityskerrointa (R² tai r-neliö) on tilastollinen mitta regressiomallissa, joka määrittää varianssin osuuden riippuvaisessa, jota käytetään selittämään astetta mitkä syötemuuttujat (ennustavat muuttujat) selittävät lähtömuuttujien (ennustetut muuttujat) vaihtelun. Se vaihtelee välillä 0 - 1. Esimerkiksi, jos R-neliö on 0,9, se osoittaa, että 90% lähtömuuttujien vaihteluista selitetään tulomuuttujilla. Yleisesti ottaen suurempi R-neliö osoittaa parempaa sopivuutta malliin. Harkitse seuraavaa kaaviota:
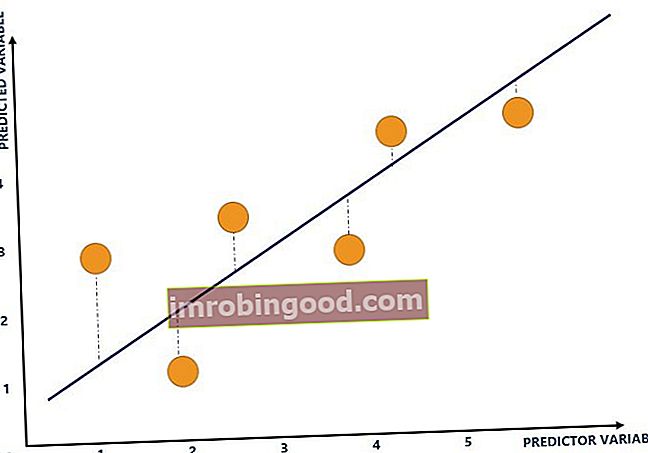
Sininen viiva viittaa parhaiten sopivaan linjaan ja osoittaa muuttujien välisen suhteen. Linja lasketaan regressioanalyysillä. Regressioanalyysi Regressioanalyysi on joukko tilastollisia menetelmiä, joita käytetään riippuvaisen muuttujan ja yhden tai useamman itsenäisen muuttujan välisten suhteiden estimointiin. Sitä voidaan käyttää muuttujien välisen suhteen vahvuuden arviointiin ja niiden välisen tulevan suhteen mallintamiseen. ja se on piirretty sinne, missä keltaisten pisteiden pystysuorat etäisyydet (siniset katkoviivat) parhaaseen sovitusviivaan on minimoitu.
Keltaiset pisteet viittaavat tulo- ja lähtömuuttujien käyrään. Syöttömuuttuja piirretään x-akselille, kun taas lähtömuuttuja piirretään y-akselille. Esimerkiksi yllä oleva kaavio koostuu seuraavasta tietojoukosta:

Siniset katkoviivat viittaavat tulo- ja lähtömuuttujien käyrän etäisyyteen parhaiten sopivasta linjasta. R-neliö saadaan kaikkien keltaisten pisteiden etäisyydestä parhaiten sopivan linjan (sininen viiva). Esimerkiksi seuraava kaavio havainnollistaa R-neliötä 1:

R-neliön ongelmat
R-neliöön liittyy luontainen ongelma - lisäpanosmuuttujat saavat R-neliön pysymään samana tai kasvamaan (tämä johtuu siitä, kuinka R-neliö lasketaan matemaattisesti). Siksi, vaikka lisäsyöttömuuttujilla ei olisikaan suhdetta lähtömuuttujiin, R-neliö kasvaa. Alla on esimerkki, joka selittää tällaisen tapahtuman.
Oikean R-neliön ymmärtäminen
Pohjimmiltaan, oikaistu R-neliö tarkastelee, vaikuttavatko muut syötemuuttujat malliin. Harkitse esimerkkiä pizzan omistajan keräämien tietojen avulla, kuten alla on esitetty:
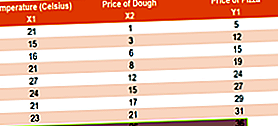
Oletetaan, että pizzan omistaja suorittaa kaksi regressiota:
Regressio 1: Taikinan hinta (syöttömuuttuja), Pizza hinta (muuttuja)
Regressio 1 tuottaa R-neliön 0,9557 ja säädetyn R-neliön 0,9493.
Regressio 2: Lämpötila (syöttömuuttuja 1), Taikinan hinta (syöttömuuttuja 2), Pizza-hinta (muuttuja)
Regressio 2 tuottaa R-neliön 0,9573 ja säädetyn R-neliön 0,9431.
Vaikka lämpötilan ei pitäisi olla ennustavaa voimaa pizzan hinnalle, R-neliö nousi 0,9557: stä (regressio 1) arvoon 0,9573 (regressio 2). Henkilö voi uskoa, että Regressio 2: lla on suurempi ennustekyky, koska R-neliö on suurempi. Vaikka lämpötilan syöttömuuttuja on hyödytön pizzan hinnan ennustamisessa, se lisäsi R-neliötä. Tässä säädetty R-neliö tulee sisään.
Säädetty R-neliö tarkastelee, vaikuttavatko muut syötemuuttujat malliin. Oikaistu R-neliö regressiossa 1 oli 0,9493 verrattuna oikaistuun r-neliöön regressiossa 2 0,9493. Siksi säädetty R-neliö pystyy tunnistamaan, että lämpötilan syöttömuuttuja ei ole hyödyllinen selitettäessä lähtömuuttujaa (pizzan hinta). Tällöin oikaistu R-neliö viittaa mallin luojaan käyttämään Regressiota 1 Regressio 2: n sijasta.
Esimerkki säädetystä R-neliöstä
Harkitse kahta mallia:
- Malli 1 käyttää tulomuuttujia X1, X2 ja X3 ennustamaan Y1.
- Malli 2 käyttää tulomuuttujia X1 ja X2 ennustamaan Y1.
Mitä mallia tulisi käyttää? Tiedot molemmista malleista ovat alla:

Vertaamalla R-neliötä mallin 1 ja mallin 2 välillä, R-neliö ennustaa, että malli 1 on parempi malli, koska sillä on suurempi selittävä voima (0,5923 mallissa 1 vs. 0,5612 mallissa 2).
Verrattaessa R-neliötä mallin 1 ja mallin 2 välillä, säädetty R-neliö ennustaa, että tulomuuttuja X3 auttaa selittämään lähtömuuttujaa Y1 (0,4231 mallissa 1 ja 0,3512 mallissa 2).
Sellaisena tulisi käyttää mallia 1, koska X3-lisämuuttuja auttaa selittämään lähtömuuttujaa Y1.
Lisäresurssit
Finance tarjoaa Financial Modeling & Valuation Analyst (FMVA) ™ FMVA® -sertifikaatin. Liity 350 600+ opiskelijaan, jotka työskentelevät yrityksissä, kuten Amazon, J.P.Morgan ja Ferrari -sertifikaattiohjelmassa, niille, jotka haluavat viedä uransa seuraavalle tasolle. Seuraavat rahoitusresurssit ovat hyödyllisiä oppimisen jatkamiseksi ja urasi edistämiseksi:
- Rahoituksen perustilastokäsitteet Rahoituksen perustilastokäsitteet Tilastojen vahva tuntemus on ensiarvoisen tärkeää, jotta voimme paremmin ymmärtää taloutta. Lisäksi tilastokonseptit voivat auttaa sijoittajia seuraamaan
- Korkea-matala menetelmä vs. regressioanalyysi Korkea matala -menetelmä vs. regressioanalyysi Korkea matala -menetelmä ja regressioanalyysi ovat kaksi pääasiallista kustannusarviointimenetelmää, joita käytetään kiinteiden ja muuttuvien kustannusten määrän arvioimisessa. Yleensä johtajien on jaettava sekakustannukset kiinteiksi ja muuttuviksi osiksi ennustamaan ja suunnittelemaan tulevaisuutta.
- Riippumaton muuttuja Riippumaton muuttuja Riippumaton muuttuja on syöte, oletus tai ohjain, jota muutetaan sen arvioimiseksi, miten se vaikuttaa riippuvaan muuttujaan (lopputulokseen).
- Taloudellisen analyysin tyypit Taloudellisen analyysin tyypit Taloudelliseen analyysiin sisältyy taloudellisten tietojen käyttäminen yrityksen suorituskyvyn arvioimiseen ja suositusten antamiseen siitä, miten se voi parantaa tulevaisuudessa. Talousanalyytikot työskentelevät pääasiassa Excelissä laskentataulukon avulla historiallisten tietojen analysointiin ja ennusteiden tekemiseen Talousanalyysin tyypit