LASSO, lyhenne sanoista Least Absolute Shrinkage and Selection Operator, on tilastollinen kaava, jonka päätarkoitus on ominaisuuksien valinta ja tietomallien laillistaminen. Menetelmän otti ensimmäisen kerran käyttöön vuonna 1996 tilastoprofessori Robert Tibshirani. LASSO tuo parametrit mallin summaan antamalla sille ylärajan, joka toimii rajoituksena summalle sisällyttää absoluuttiset parametrit sallitulle alueelle.
LASSO-menetelmä normalisoi malliparametrit kutistamalla regressiokertoimia, pienentämällä jotkut niistä nollaan. Ominaisuuden valintavaihe tapahtuu kutistumisen jälkeen, jolloin jokainen nollasta poikkeava arvo valitaan mallissa käytettäväksi. Tämä menetelmä on merkittävä ennustevirheiden minimoinnissa, jotka ovat yleisiä tilastollisissa malleissa. Kvantitatiivinen analyysi Kvantitatiivinen analyysi on prosessi, jolla kerätään ja arvioidaan mitattavissa olevia ja todennettavissa olevia tietoja, kuten tulot, markkinaosuus ja palkat, jotta voidaan ymmärtää liiketoimintaa. Tietotekniikan aikakaudella kvantitatiivista analyysia pidetään ensisijaisena lähestymistapana tietoon perustuvien päätösten tekemisessä. .
LASSO tarjoaa malleja, joilla on suuri ennustetarkkuus. Tarkkuus kasvaa, koska menetelmä sisältää kertoimien kutistumisen, mikä vastineeksi vähentää varianssia ja minimoi harhaa. Se toimii parhaiten, kun havaintojen määrä on pieni ja ominaisuuksien määrä on suuri. Se luottaa vahvasti parametriin λ, joka on kutistumisen ohjaava tekijä. Mitä suurempi λ tulee, sitä enemmän kertoimet pakotetaan olemaan nolla.
Kun λ on yhtä suuri kuin nolla, mallista tulee tavallisen pienimmän neliön regressio. Tämän seurauksena, kun λ kasvaa, varianssi pienenee merkittävästi ja myös tuloksen puolueellisuus kasvaa. Lasso on myös hyödyllinen työkalu eliminoimaan kaikki muuttujat, joilla ei ole merkitystä ja jotka eivät liity vastemuuttujaan.
LASSO tilastollisissa lineaarisissa malleissa
Tilastollinen malli on tosielämän matemaattinen esitys ongelmasta. Mallin tulisi ilmaista ongelma mahdollisimman lähellä todellista maailmaa ja tehdä siitä yksinkertainen ja helposti ymmärrettävä. Malli koostuu selittävistä ja vastemuuttujista.
selittävä muuttuja on riippumaton muuttuja, joka on tutkijan harkinnan mukaan. Riippumattomat muuttujat ovat mallin syötteitä, joita tutkija voi mitata määrittääkseen niiden vaikutuksen mallin tuloksiin.
vastemuuttuja on riippuva muuttuja Riippuva muuttuja Riippuva muuttuja on muuttuja, joka muuttuu riippuen toisen muuttujan arvosta, nimeltään itsenäinen muuttuja. joka muodostaa kokeen pääkohteen. Se muodostaa kokeen tuloksen, joka voi olla yksittäinen tulos yksimuuttujaisten mallien tapauksessa tai, jos kyseessä on monimuuttujainen malli, useita tuloksia.
LASSO on olennainen osa mallin rakennusprosessia, erityisesti ominaisuuksien valintaa käyttämällä. Ominaisuuksien valintavaihe auttaa selittävien muuttujien valinnassa, jotka ovat riippumattomia muuttujia ja siten mallin syöttömuuttujia.
Tulomuuttujat ovat tärkeitä elementtejä, jotka määrittävät mallin tuotoksen ja auttavat mittaamaan niiden vaikutusta vastemuuttujiin. Oikeiden muuttujien valitseminen määrittää mallin tarkkuuden. LASSO: n ominaisuuksien valintavaihe auttaa muuttujien oikeassa valinnassa.
Arviointi LASSO: n kanssa
Tilastomallit käyttävät LASSO: ta tarkan muuttujien valinnan ja laillistamisen suhteen. Lineaarisessa regressioregressioanalyysissä regressioanalyysi on joukko tilastollisia menetelmiä, joita käytetään riippuvan muuttujan ja yhden tai useamman itsenäisen muuttujan välisten suhteiden estimointiin. Sitä voidaan käyttää muuttujien välisen suhteen vahvuuden arviointiin ja niiden välisen tulevan suhteen mallintamiseen. Esimerkiksi LASSO ottaa käyttöön ylärajan neliöiden summalle, mikä minimoi mallissa esiintyvät virheet. LASSO-estimaattori riippuu parametrista λ.
Parametri λ säätää kutistumisen voimakkuutta, jolloin X: n kasvu johtaa kutistumisen lisääntymiseen. Kaikkien kertoimien summan yläraja on kääntäen verrannollinen parametriin λ. Kun yläraja nousee, parametri λ pienenee. Kun yläraja pienenee, parametri λ kasvaa samanaikaisesti.
Kun yläraja kasvaa kohti ääretöntä, parametri λ lähestyy nollaa, mikä muuntaa kokeen tavallisiksi pienimmiksi neliöiksi, jossa parametri λ on aina yhtä suuri kuin nolla. Kun ylärajakertoimet lähestyvät nollaa, parametrin λ arvo kasvaa kohti ääretöntä.
LASSO-geometria
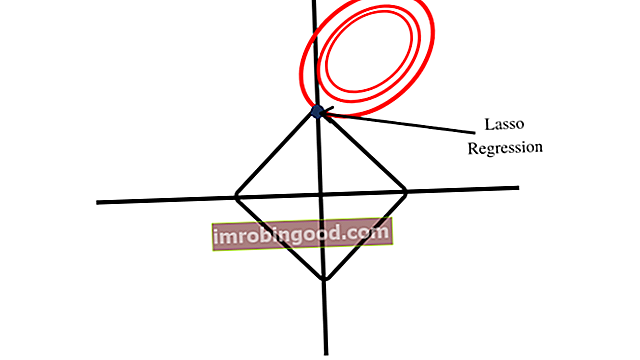
LASSO muodostaa kaavion timantin muodon rajoitusalueelleen, kuten alla olevassa kuvassa näkyy. Timantin muoto sisältää kulmat, toisin kuin harjanteen regressiosta muodostuva pyöreä muoto. Ensimmäisen pisteen läheisyys kulmaan osoittaa, että mallissa on yksi kerroin, joka on nolla.
Harjanteen regressiorajoitusalue muodostaa pyöreän muodon, joka ei sisällä kulmia, jotka olisivat samanlaisia kuin LASSO-rajoitusalueen muodostamat kulmat piirrettäessä. Harjanteen regressiokertoimet eivät sen vuoksi voi olla yhtä suuria kuin nolla.
Painotettu LASSO
Painotettu LASSO on tulos tutkijasta, joka rankaisee regressiokertoimia erikseen. Tämä tarkoittaa sitä, että sen sijaan, että rangaistaan yhteistä parametria λ kaikille kertoimille, kertoimista rangaistaan erikseen käyttäen erilaisia parametreja.
Painot voidaan määrittää käyttämällä LASSO-algoritmia, jotta painot voidaan määrittää tarkalle mallinnukselle. Samanlainen regressiokertoimien painotus on osuuskunta LASSO, jossa kertoimet rangaistaan ryhmissä, joiden katsotaan olevan samanlaisia.
Lisäresurssit
Rahoitus on Certified Banking & Credit Analyst (CBCA) ™ CBCA ™ -sertifikaatin virallinen toimittaja. Certified Banking & Credit Analyst (CBCA) ™ -sertifikaatti on maailmanlaajuinen luottotietojen analyytikoiden standardi, joka kattaa rahoituksen, kirjanpidon, luottotutkimukset, kassavirta-analyysit kovenanttimallinnus, lainojen takaisinmaksut ja paljon muuta. sertifiointiohjelma, joka on suunniteltu muuttamaan kuka tahansa maailmanluokan rahoitusanalyytikkoksi.
Jotta voisit oppia ja kehittää taloudellisen analyysin tietosi, suosittelemme alla olevia lisärahoitusresursseja:
- Ennustamismenetelmät Ennustamismenetelmät Suosituimmat ennustamismenetelmät. Tässä artikkelissa selitämme neljän tyyppisiä tulojen ennustamismenetelmiä, joita rahoitusanalyytikot käyttävät tulojen ennustamiseen.
- Riippumaton muuttuja Riippumaton muuttuja Riippumaton muuttuja on syöte, oletus tai ohjain, jota muutetaan sen arvioimiseksi, miten se vaikuttaa riippuvaan muuttujaan (lopputulokseen).
- Moninkertainen lineaarinen regressio Moninkertainen lineaarinen regressio Moninkertainen lineaarinen regressio viittaa tilastolliseen tekniikkaan, jota käytetään ennustamaan riippuvan muuttujan tulos riippumattomien muuttujien arvon perusteella
- Skenaarioanalyysi Skenaarioanalyysi Skenaarioanalyysi on tekniikka, jota käytetään analysoimaan päätöksiä spekuloimalla erilaisia mahdollisia tuloksia investointeihin. Taloudellisessa mallinnuksessa tämä

